Mitigation by Crop Management

1. Avoidance of Nutrient Stress 

The efficiency of fertilizers might be lower than fifty per cent either due to mismanagement or due to reactions of the fertilizers with soil constituents. only a fraction of the fertilizer applied to the soil is taken up by the crop, the rest is either remains in the soil or lost through leaching, physical wash off, fixation by the soil, or release to the atmosphere through chemical and microbiological processes (Hera, 1996). Fertilizer losses especially of nitrogen could happen during the period of plant growth and lead to low yields than expected. This

low uptake and utilization of nutrients out of the added fertilizers results in lower production and appearance of nutrient stress symptoms. The poor efficiency of added fertilizers is mainly due to imbalance fertilization or improper management practices. Critical information on the fertilization practices like: method of fertilizer placement, time and rate of application and type of fertilizers are essential for successful yields.

There are three general main types of nitrogen fertilizers where the nitrogen in the fertilizer is found in the chemical form of: ammonium, urea and nitrate. Nitrogen in nitrate form fertilizer are soluble and highly mobile in soil. They are prone to various kinds of losses: leaching beyond the root zone in the light textured soils, denitrification in water logged conditions or short time of over irrigation (Bar-Yosef and Kafkafi, 1972). Ammonium type fertilizers usually transform in the soil within a week or two to nitrate form and the further consideration is the same as for nitrate fertilizers.

 Phosphate fertilizers, which are highly reactive, are fixed in soil and become immobile. Potassic fertilizers are less mobile, since they are adsorbed on the clay complex. The entire quantity of phosphate and potassic fertilizers are, therefore, applied in one dose at the time of sowing in annual crops. Whereas, split application of nitrogenous fertilizers increases nitrate reductase activity, uptake of nitrogen (Abrol, 1990), use efficiency (Destain et al., 1997) and grain yield (Sabbe and Batchelor, 1990).

Application of fertilizers in narrow bands beneath and by the side of the crop rows i.e. band placement is preferable when the crop needs initial good start; when the soil fertility is low; when fertilizer materials react with soil constituents leading to fixation (phosphorus) and where volatilization losses are high.

Addition of organic matter to the soil at regular periods, helps to maintain the buffer capacity of the soil to supply the essential elements after its decomposition. Organic matter in soils can be regulated through different agronomic practices such as application of compost, farmyard manure, vermicompost, green manure etc’.

2. Management of Nutrient Stress

When the soil is deficient in a particular nutrient element and the crop grown on such soil show visible deficiency symptoms, there is urgent need to correct it to improve the crop production. Methods of correcting nutrient deficiencies vary according to agro-climatic regions, the socioeconomic situations of the region, the magnitude of disorder, and nutrient element involved. A generalized description of these methods is presented in Table 2. Use of nutrient-efficient cultivars in combination with fertilizers or amendments may be the best solution for correcting nutrient disorders in field crops, but this will vary according to situation. Fertilizer recommendations are usually based on the results of field trials in which crop response to various rates of fertilizer application is determined. Such response curves provide relationships between yield and the amount of fertilizer required for a particular crop grown in a specific agro-climatic region.

In a standing crop, if the nutrient deficiency is confirmed, the foliar application of selected nutrients by means of spray is a quick way to get rid of stress symptoms and avoiding yield loss. Foliar fertilization of macro and micronutrients is best practice whenever nutrient uptake through the roots is restricted due to adverse growing conditions (El-Fouly and El-Sayed, 1997), when topsoil is dry particularly in semiarid regions (Grundon, 1980), under saline soils (El-Fouly and Salama, 1999), and when root activity decreases during reproductive stage (Ikeda et al., 1991). In calcareous soils iron availability is generally very low and chlorosis is quite common, foliar spraying under these conditions is very beneficial (Horesh and Levy, 1981). For example, iron chlorosis was corrected by foliar application of 0.1% aqueous solution of Fe applied at 2 Kg Fe ha^-1, either as iron citrate or as iron sulfate + 400 g ha^-1 citric acid (0.02%), in four equal splits at 30, 45, 60 and 75 days after emergence in groundnut (Singh and Joshi, 1997). Manganese deficiency in such soils is also widespread and two or more sprays may be required within a growing season (Gettier et al., 1985). Not all crops respond equally to foliar nutrition and the nutrient elements differ in their rate of uptake through foliage and the degree of mobility within the plant once absorbed (Table 3).

 Mitigation by Plant Resistance

Nutrient concentration and uptake by different plant genotypes are the most important criteria for identifying the existing genetic specificity of plant nutrition (Saric, 1987). The tolerance in a given plant species or genotype to nutrient stress is closely related to its nutrient use efficiency. Genotypic differences in nutrient use efficiency are linked with root nutrient acquisition capacity, or with utilization by the plant, or both. Various plant species have developed morphological and/or physiological mechanisms to improve acquisition and use efficiency of mineral nutrients when grown on poor, infertile soils (Romeheld, 1998). By such mechanisms plants achieve nutrient deficiency stress tolerance. However, sometimes the ability to adapt to stress is limited, depending on the intensity and duration of stress. For example, some nutrient stress factors, when operating for a long period, can result in inhibited growth and root physiological processes responsible for nutrient uptake with the consequence of an impaired capability for adaptation and stress tolerance.

For a given genotype, nutrient use efficiency is reflected by the ability to produce a high yield in a soil that is limiting in one or more mineral nutrients for a standard genotype (Graham, 1984). The efficiency should be compared under stress and adequate nutrient supply to verify plant species or genotypic differences in nutrient utilization under sub-optimal and optimal conditions. The differential response of genotypes to nutrient stress is related to uptake, transport and utilization pattern of nutrients within plants (Fig.2). Isolation of intra-species differences in capacity for growth under specific nutritional conditions, particularly under nutritional stress is a critical aspect in nutritional plant genetics. A wide range of morphological, anatomical and physiological plant traits can be responsible for variations in response to nutrient stress within a plant species. Such traits can function either within or outside the plant to affect nutrient availability, absorption, translocation or utilization. Some physiological and morphological plant features controlling plant resistance to nutritional stress are given in Table 4.

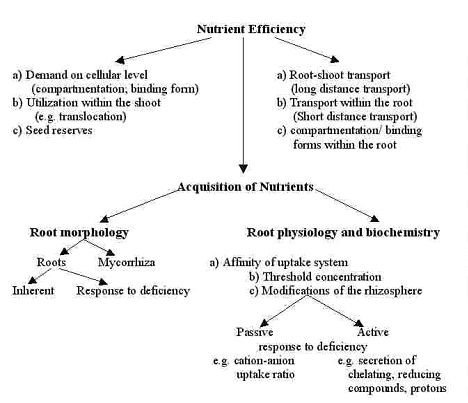
The acquisition of nutrients by plant roots plays the most important role in tolerance to nutrient stress. Genotypes can differ widely in both the affinity of uptake and the threshold concentration, for example, the uptake of phosphorus in corn inbred lines (Schenk and Barber, 1979). The differences in their ability to grow in soils of low phosphorus status might be attributed to several factors including differential influx rates, root length/shoot weight ratios (Fohse et al., 1988) or root system morphology and root hair density (Randall, 1995). Among the more important factors is the role of root exudates in making available soil P ‘fixed’ in forms such as iron or aluminum phosphate. White lupin and pigeon pea are well adapted to acidic P-deficient soils (Hocking et al., 1997). White lupin forms develop proteoid roots (bottlebrush-like clusters of rootlets covered with a dense mat of root hairs) which are considered to be a response to low P availability (Marschner, 1986). Proteoid roots of white lupin secrete citric acid which solubilizes ‘fixed’ P (Gardner et al., 1983; Gerke et al.,1994), thus increasing P uptake by the plant. For pigeon pea, secretion of piscidic, malonic and oxalic acids appears to be the mechanism by which this species is able to release P from iron and aluminum phosphates (Otani et al., 1996). Screening of tolerant Medicago sativa and Lablab purpureus germplasm under phosphorus stress condition was carried out by Mugwira and Haque (1993a and b) based on their root and shoot growth.

Genetic differences in K uptake and utilization efficiency in field crop cultivars have also been observed (Glass et al., 1981). Growth response of 20 wheat genotypes were compared by Gill et al. (1997) under deficient (0.6 mM) and adequate (3.0 mM) K levels in solution cultures. Substantial and significant differences due to K-stress were obvious among genotypes for shoot dry weight, relative reduction in shoot dry weight, root dry weight, and root/shoot ratio. Rengel (1997) screened wheat genotypes tolerant to Zn and Mn stress. Wheat genotypes tolerant to Zn deficiency released greater amounts of phytosiderophore, 2-deoxymugineic acid, than the sensitive genotypes. In addition, Zn deficiency increased the numbers of fluorescent pseudomonas in rhizosphere of all wheat genotypes tested, but the effect was particularly obvious for genotypes tolerant to Zn deficiency. Under Mn stress, wheat genotypes tolerant of Mn deficiency had a greater ratio of Mn-reducers to Mn-oxidizers in the rhizosphere compared to sensitive genotypes. Mn-efficient durum wheat genotypes had greater Mn uptake from Mn deficient soil, produced higher grain yield, relative grain yield and above ground biomass and generally maintained higher seed Mn concentration (Khabaz-Saberi et al., 1997).

The Fe efficient groundnut cultivar ‘ICGV-86031’ released more hydrogen ions and reductants from its roots under iron deficiency stress treatment, maintained higher leaf Fe and had less chlorosis than the Fe-inefficient cultivar ‘TCGS-37’ (Reddy et al., 1997). There are also large differences in tolerance to Fe deficiency among field grown wheat genotypes (Hanson et al., 1996).

Genetic control of Cu efficiency has been located on the long arm of the rye chromosome 5 and has been applied to wheat breeding for CU efficiency (Podlesak et al., 1990).

Similar, increase in Cu efficiency was observed by Graham (1984) in spring form of rye (Secale cereale L.) and genetically manipulated wheat. Wheat genotypes differ in tolerance to Zn deficiency (Graham et al., 1992; Cakmak et al., 1996a), with durum wheat being generally less tolerant than bread wheat (Rengel and Graham, 1995; Cakmak et al., 1996). Tolerance of bread wheat genotypes to Zn and Fe deficiency was expressed in shoot dry weight and relative shoot growth as compared with to sensitive genotypes (Rengel and Romheld, 2000).

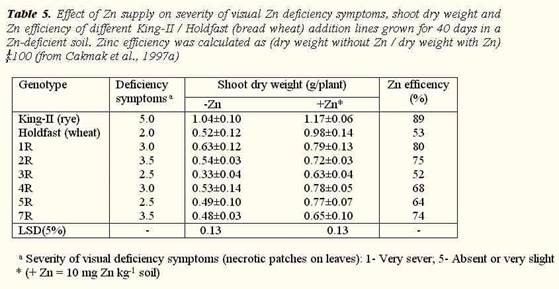
Cereal species, as well as genotypes of a given cereal greatly differ in adaptation to Zn-deficient conditions. The susceptibility of cereals to Zn deficiency was found to decline in the order: durum wheat > oat > bread wheat > barley > triticale > rye. Among the cereals, rye showed an exceptionally high Zn efficiency. Biomass production and grain yield of rye was not affected under severe Zn-deficient conditions (Cakmak et al., 1997b). Several mechanisms constitute the physiological bases of Zn efficiency. These are enhancement of root growth (Dong et al., 1995), root uptake and root-to-shoot translocation of Zn (Cakmak et al., 1996a; Rengel and Graham, 1996), release of Zn-mobilizing phytosiderophores from roots (Cakmak et al., 1996b; Erenoglu et al., 1996) and internal utilization of Zn (Cakmak et al., 1996b; Rengel, 1995). Use of disomic wheat-rye addition lines (Triticum aestivum L., cv. Holdfast-Secale cereale L., cv. King-II) increases Zn efficiency (Table 5). The addition of rye chromosomes, particularly 1R, 2R and 7R, into Holdfast reduced the severity of deficiency symptoms (Cakmak et al., 1997a). Transgenic plants have improved nutrient efficiency and resistant to nutrient stress. This was found for copper in wheat (Graham et al., 1987); boron and phosphorus in tobacco (Brown et al., 1999; Lopez-Bucio et al., 2000).

The molecular approach to breeding of mineral deficiency resistance and mineral efficiency is now receiving increasing attention. QTLs (quantitative trait loci) controlling Phosphorus efficiency were identified in rice and maize. Transgenic tobaccos overexpressing ferritin in the plastids or in the cytoplasm resulted in higher leaf concentration of iron, manganese and zinc (see #4791 in this site reference database). Tobacco transformation over expressing the antioxidant superoxide dismutase had greater manganese deficiency resistance (#4512).

Related Publications

• Principles of Plant Nutrition, by K. Mengel and E. A. Kirkby. (International Potash Institute, Berne, Switzerland).
• Diagnosis of Mineral Disorders in Plants. Vol. 1, Principles, by C. Bould, E. H. Hewitt, and P. Needham. (Chemical Publishing, New York, 1984).
• Diagnosis of Mineral Disorders in Plants. Vol. 2, Vegetables, by A. Scarfe and Mary Turner. (Chemical Publishing, New York, 1984).
• Plant Analysis Handbook, by J. Benton Jones Jr., B. Wolf, and H. A. Mills. (Micro-Macro Publishing, Athens, GA, 1991).
• Nutritional Disorders of Plants, Ed. by, Werner Bergmann. (Gustav Fischer Verlag, Gena, Germany, 1992).
• Nutrient Deficiencies and Toxicities in Crop Plants, Ed. by, William F. Bennett. (The American Phytopathological Society, St. Paul Minnesota, 1993).
• Mineral Nutrition of Higher Plants2^nd Ed. by, H. Marschner (Academic Press, London, 1997).
• Growth and nutrition of field crops2^nd Ed. by, N. K. Fageria; V. C. Baligar, and C. A. Jones. (Marcel Dekker, Inc. New York, 1997).

Reviews

• Raun W.R. Johnson G.V.  1999. Improving nitrogen use efficiency for cereal production  Agron. J. 91:357-363.
• Liptay A. Arevalo A.E.  2000. Plant mineral accumulation, use and transport during the life cycle of plants: A review Can. J. Plant Sci. 80:29-38.

Cited Literature

Abadia, A.; Sanz, M.; Rivas, J.; Abadia, J. and De, L. 1988. Pear yellowness; an atypical form of iron chlorosis. Acta Horticulturae. 256: 177-181.

Abrol, Y. P. 1990. Pattern of nitrate assimilation and grain nitrogen yield in field-grown wheat (Triticum aestivum). In: M. L. van Beusichem (Ed.), Plant nutrition- physiology and applications, Kluwer Academic Publishers, Dordrecht. 773-778.

Adams, P. and El-Gizawy, A.M. 1988. Effect of calcium stress on the calcium status of tomatoes grown in NFT. Acta Horticulturae. 22: 15-22.

Anoop, E.V.; Gopikumar, K. and Babu, L.C. 1998. Visual symptoms and chlorophyll production of Ailanthus triphysa seedlings in response to nutrient deficiency. J. Tropical Forest Sci. 10(3): 304-311.

Arnold, N.; Chong, C. and Binns, M. 1986. Seasonal nutrient contents in grey and non-grey flue-cured tobacco. Beitrage zur Tabakforschung Int. 13(5): 265-269.

Arnon, D.J. 1954. Trace elements in plant physiology. In ‘Chronica Botanica’ (Ed. T. Wallace), Waltham, Massachusetts.

Balakrishnan, K. 1999. Studies on nutrients deficiency symptoms in chilli (Capsicum annum L.). Indian J. Plant Physiol. 4(3): 229-231.

Baranwal, V.K.; Manikandan, P.; Ray, A.K. 1989. Crown choking disorder of coconut: a case of boron deficiency. J. Plantation Crops. 17(2): 114-120.

Bar-Yosef, B. and Kafkafi, U. 1972.  Rates  of  growth and nutrient uptake of irrigated corn as      affected by N and P fertilization.  Soil  Sci.  Soc.  Am.  Proc. 36: 931-936.

Bennett, W. F. 1993. Plant Nutrient Utilization and Diagnostic Plant Symptoms, In: Nutrient Deficiencies and Toxicities in Crop Plants. The American Phytopathological Society, St. Paul Minnesota, pp. 1-7.

Bernier, B. and Brazeau, M. 1988. Nutrient deficiency symptoms associated with sugar maple dieback and decline in the Quebec Appalachians. Canadian J. Forest Res. 18(6): 762-767.

Besford, R.T. 1978. Effect of sodium in the nutrient medium on the incidence of potassium deficiency symptoms in tomato plants. Plant and Soil. 50(2): 427-432.

Brown, P. H.; Nacer, B.; Hening, H. and Abhaya, D. 1999. Transgenically enhanced sorbital synthesis facilitates phloem boron transport and increase tolerance of tobacco to boron deficiency. Plant Physiol. 119: 17-20.

Cakmak, I.; Sary, N.; Marschner, H.; Kalayci, M.; Yilmaz, A.; Eker, S. and Gulut, K. Y. 1996a. Dry matter production and distribution of Zn in bread and durum wheat genotypes differing in Zn efficiency. Plant and Soil. 180: 173-181.

Cakmak, I.; Sary, N.; Marschner, H.; Ekiz, H.; Kalayc, A.; Yilmaz, A. and Braun, H. J. 1996b. Release of phytosiderophores in bread and durum wheat genotypes differing in Zn efficiency. Plant and Soil. 180: 183-189.

Cakmak, I.; Derici, R.; Torun, B. Tolay, I.; Braun, H. J. and Schlegel, R. 1997a. Role of rye chromosome in improvement of zinc efficiency in wheat and triticale. In: Plant Nutrition- for sustainable food production and environment, T. Ando et. al. (Eds), Kluwer Academic Publishers, Tokyo. 237-241.

Cakmak, I.; Ekiz, H.; Yilmaz, A.; Torun, B.; Kolele, N.; Gultekin, I.; Alkan, A. and Eker, S. 1997b. Differential response of rye, triticale, bread wheat, and durum wheat to Zn deficiency in calcareous soils. Plant and Soil. 188: 1-10.

C F A, 1985. Methods of applying fertilizer. In: Western Fertilizer Handbook (8th Eds). Interstate Publishers, Inc. Danville, USA. 161-182.

Conover, C.A.; Poole, R.T. and Satterthwaite, L.N. 1991. Soil temperature and copper rate affect growth and copper deficiency of Aglaonema commutatum ‘Fransher’. J. Environmental Hort. 9(2): 65-67. 

Cox, D.A. and Bartley, G.C. 1987. Lime, molybdenum and cultivars effects on molybdenum deficiency of poinsettia. Res. Report Series Albama Agric. Expt. Station, Auburn Univ. publ.1988, No. 5, 13.

Cox, D.A. 1992. Poinsettia cultivars differs in their response to molybdenum deficiency. HortScience. 27(8): 892-893.

Dell, B.1994. Copper nutrition of Eucalyptus maculata Hook seedlings: requirements for growth, distribution of copper and the diagnosis of copper deficiency. Plant and Soil. 167(2): 181-187.

Destain, J. P.; Bodson, B.; Herman, J. L.; Francois, E. and Franc, J. 1997. Uptake and efficiency of split applications of nitrogen fertilizer in winter wheat. In: Plant Nutrition- for sustainable food production and environment, T. Ando et. al. (Eds), Kluwer Academic Publishers, Tokyo. 633-634.

Dong, B.; Rengel, Z. and Graham, R. D. 1995. Root morphology of wheat genotypes differing in Zn efficiency. J. Plant Nutr. 18: 2761-2773.   

Duval, L ; More, E. and Sicot, A. 1991. Observations on molybdenum deficiency in cauliflower in Brittany. Comtes Rendus de I Academic d Agriculture de France. 78(1): 27-34.

Edwards, J.H. and Horton, B. D. 1979. Response of peach seedlings to calcium concentration in nutrients solution. J. American Soc. Hort. Sci. 104(1): 97-99.

El-Fouly, M. M. and El-Sayed, A. A. 1997. Foliar fertilization; an environmentally friendly application of fertilizers. In: Mortvedt, J. J. (Ed.) Proceedings of Dahlia Greidinger International Symposium on Fertilization and the Environment, Technian Haifa. pp.346-358.

Erenoglu, B.; Cakmak, I.; Marschner, H.; Romeheld, V.; Eker, S.; Daghan, H.; Kalaycy, M. and Ekiz, H. 1996. Phytosiderophores release does not relate well to zinc efficiency in different bread wheat genotypes. J. Plant. Nutr. 19: 1569-1580.

Fageria, N. K.; Baligar, V. C. and Jones, C. A. 1997a. Growth and nutrition of field crops 2^nd Ed. Marcel Dekker, Inc. New York. p. 85.

Fageria, N. K.; Baligar, V. C. and Jones, C. A. 1997b. Growth and nutrition of field crops 2^nd Ed. Marcel Dekker, Inc. New York. p. 127.

Fohse, D.; Classen, N. and Jungk, A. 1988. Phosphorus efficiency of plants. I. External and internal P requirement and P uptake efficiency of different plant species. Plant and Soil. 11: 101-109.

Fonts, R.L.F. and Cox, F.R. 1998. Zinc toxicity in soybean grown at high iron concentration in nutrient solution. J. Plant Nut. 21(8): 1723-1730.

Fords, E.M. 1979. The distribution of calcium in mature apple fruits having bitter pit disorder. J. Horticultural Sci. 54(1): 91-92.

Friend, A.L.; Eide, M.R. and Hinckley, T.M. 1990. Nitrogen stress alters root proliferation in Douglas-fir seedlings. Canadian J. Forest Res. 20(9): 1524-1529.

Gardner,W. K.; Barber, D. A. and Parbery, D. G. 1983. The acquisition of phosphorus by Lupinus albus L. III. The probable mechanism by which phosphorus  movement in the soil/root interface is enhanced. Plant and Soil. 70: 107-124.

Gautam, R.C. and Sharma, K.C. 1982. Zinc deficiency (Khaira) as influenced by planting scheme and plant densities in rice. Plant and Soil. 69(2): 299-300.

Gerendás, J. and Sattelmacher, B. 1997. Significance of Ni supply for growth, urease activity and the concentrations of urea, amino acids and mineral nutrients of urea-grown plants. Plant and Soil. 190: 153-162.

Gerke, J.; Romer, W. and Jungk, A. 1994. The excretion of citric and malic acid by proteoid roots of Lupinus albus L.; effects on the soil solution concentrations of phosphate, iron and aluminium in the proteoid rhizosphere in samples of an Oxisol and a Luvisol. Bodenk. 157: 289-294.

Gerloff, G. C. 1987. Intact-plant screening for tolerance of nutrient deficiency stress. Plant and Soil. 99: 3-16.

Gill, M. A.; Ahmad, M. I. and Yaseen, M. 1997. Potassium-deficiency stress tolerance and potassium utilization efficiency in wheat genotypes. In: Plant Nutrition- for sustainable food production and environment, T. Ando et. al. (Eds), Kluwer Academic Publishers, Tokyo. 321-322. 

Glass, A. D. M.; Siddiqui, M.Y. and Giles. K.I. 1981. Plant Physiol. 68: 457-459.

Graham, R. D. 1984. Breeding for nutritional characteristic in cereals. In ‘Advances in Plant Nutirtion’ (P. B. Tinker and A. Lauchli, eds.), Vol.1, pp. 57-102. Praeger, New York.

Graham, R. D.; Ascher, J. S.; Ellis, P. A. E. and Shepherd, K. W. 1987. Transfer to wheat of the copper efficiency factor carried on rye chromosome arm 5RL. Plant and Soil. 99: 107-114.

Graham, R. D.; Ascher, J. S. and Hynes, S. C. 1992. Selecting Zn efficient cereal genotypes for soils  of low Zn status. Plant and Soil. 146: 241-250.

Grundon, N. J. 1980. Effectiveness of soil-dressing and foliar spray of copper sulfate in correcting copper deficiency of wheat (Triticum aestivum) in Queensland. Aus. J. Exp. Agric. Anim. Husb. 20: 717-723.

Gupta, U.C. and  Gupta, U.C. 1997. Symptoms of molybdenum deficiency and toxicity in crops. Molybdenum in Agriculture. 160-170.

Gupta, U.C. and Sanderson, J.B. 1993. Effect of S, Ca and B on tissue nutrient concentration and potato yield. J. Plant Nut. 16(6): 1013-1023.

Hamy, A. 1983. Effect of phosphorus deficiency on pigments of barley leaves. Compets Rendus des Seances de l Academie d Agriculture de France. 69(12): 935-943.

Hansen, N. C.;  Jolley, V. D.; Berg, W. A.; Hodges, M. E. and Krenzer, E. G. 1996. Phytosiderophore release related to susceptibility of wheat to iron deficiency. Crop Sci. 36: 1473-1476.

Hanson, E. 1993. Apples and Pears, In: Nutrient Deficiencies and Toxicities in Crop Plants. The American Phytopathological Society, St. Paul Minnesota, pp. 1-7.

Hera, C. 1996. The role of inorganic fertilizers and their management practices. In:  C. Rodriguez-Barrueco (Ed.), Fertilizer and Environment, Kluwer Academic Publishers, Dordrecht, 131-149.

Hoching, P. J.; Keerhisinghe, G.; Smith, F. W. and Randall, P.J. 1997. Comparison of the ability of different crop species to access poorly-available soil phosphorus. In: Plant Nutrition- for sustainable food production and environment, T. Ando et. al. (Eds), Kluwer Academic Publishers, Tokyo. 305-308.

Ho, L.C.; Hand, D.J.; Fussell, M. and Papadopoulos, A.P. 1999. Improvement of tomato fruit quality by calcium nutrition. Acta Horticulturae. 481(2): 417-423.

Horesh, I. and Levy, Y. 1981. Response of iron deficient citrus trees to foliar iron sprays with a low surface tension surfactant. Sci. Hortic. (Amsterdam) 15: 227-233.

Jacques, D.J. ; Boerner, R.E.J. and Peterson, J.C. 1990. Effect of Ca supply and stress on uptake and translocation of Ca in two poinsettia cultivars. Envr. & Expt. Botany. 30(4): 525-531.

Jean-Baptist, I.; Morard, P.; Bernadac, A. and Papadopoulos, A.P. 1999. Effects of temporary calcium deficiency on the incidence of a nutritional disorder in melon. Acta Horticulturae. 481(1): 417-423.

Jolly, V.D. ; Brown, J.C. and Nugent, P.E. 1991. A genetically related response to iron deficiency stress in muskmelon. Plant & Soil. 130(1-2): 87-92.

Kafkafi,  U.,  Walerstein,  I.  and  Feigenbaum, S. 1971.  Effect of  potassium  nitrate and  ammonium nitrate on  the  growth,  cation  uptake  and  water requirement  of tomato grown in sand soil culture. Israel J. Agric. Res. 21:13-30.

Khabaz-Saberi, H.; Robin, D.; Graham, R. D. and Rathjen, A. J. 1997. Genotypic variation for Mn efficiency in durum wheat (Triticum turgidium L. var. durum). In: Plant Nutrition- for sustainable food production and environment, T. Ando et. al. (Eds), Kluwer Academic Publishers, Tokyo. 289-290.

Khan, H.R. ; McDonald, G.K. and Rengel, Z. 1998. Assessment of the Zn status of chickpea by plant analysis. Plant & Soil. 198(1): 1-9.

Krogmeier, M. J.; McCarty, G. W.; Shogren, D. R. and Bremner, J. M. 1991. Effect of nickel deficiency in soybeans on the phytotoxicity of foliar-applied urea. Plant and Soil. 135: 283-286.

Landsberg, E.C. 1996. Hormonal regulation of iron stress response in sunflower roots: a morphological and cytological investigation. Protoplasma. 194(1-2): 69-80.

Lopez-Bucio, J.; Marinez, de la Vega O; Guevara-Garcia and Herrera-Estrella, L. 2000. Enhanced phosphorus uptake in transgenic tobacco plants that overproduce citrate. Nature Biotechnology. 18(4): 450-453.

Makkanen, S.K. 1995. Damage by drought stress and magnesium deficiency: experiments on young spruce clones. Allgemeine Forst Zeitschrift 50(5): 263-267.

Marschner, H. 1986. Mineral Nutrition of Higher Plants. Academic Press, San Diego, California, USA. p.461.

Marschner, H. 1997a. Introduction, Definition, and Classification of Mineral Nutrients. In: Mineral Nutrition of Higher Plants 2nd Ed. Academic Press, London. pp. 3-5.

Marschner, H. 1997b. Adaptation of plants to adverse chemical soil conditions. In: Mineral Nutrition of Higher Plants 2nd Ed. Academic Press, London. pp. 596-680.

Mehrotra, S.C. and Gupta, P. 1990. Screening of chickpea ( Cicer arietinum) varieties under iron deficiency stress conditions using biochemical indicators. Indian J. Agric. Sci. 60(8): 566-568.

Miao, Y.; Jiang, Y.T.; Zeng, G.H. and Cao, J.S. 1997. Changes of Ca²⁺ compartmentation and ultrastructure in inner leaves of chinese cabbage (Brassica compasteris sp. Pekinensis olson) during the development of calcium related physiological disorder. Acta Horticulturae Sinica. 24(2): 145-149.

Monge, E.; Val, J.; Sanz, M.; Blanco, A. and Montanes, L. 1995. Calcium as a plant nutrient. Bitter pit in apple. Annale de la Estaction Experimental de Aula Dei. 21(3): 189-201.

Mugwira, L. M. and Haque, I. 1993. Screening forage and browse legume germplasm to nutrient stress I: Tolerance of Medicago sativa L. to Al and low P in soils and nutrient solution. J. Plant Nutr. 16(1): 17-35.

Mugwira, L. M. and Haque, I. 1993. Screening forage and browse legume germplasm to nutrient stress II: Tolerance of Lablab purpureus L. to acidity and low P in two acid soils. J. Plant Nutr. 16(1): 37-50.

Nachegowda, V.; Sulladmath, U.V. ; Vijyakumar, N and Subhadrabandu, S. 1992. Visual nutrient deficiency symptoms in sapota ( Manilkara achras Forsberg). Acta Horticulturae. 321: 566-573.

Nautiyal, N. ; Chaterjee, C. and Sharma, C.P. 1999. Copper stress affects grain filling in rice. Commun. Soil Sci. & Plant Analysis. 30(11-12): 1625-1632.

Nautiyal, N. ; Dubey, B.K. and Chatterjee, C. 2000. Symptoms of nutrient deficiency (N, P, Ca, Mg and S ) in sugarcane grown in refined sand. Sugarcane Intr. March.; 12-17.

Nybe, E.V. and Nair, P.C.S. 1986. Nutrient deficiency in black pepper (Piper nigrum L.). 1. Nitrogen, phosphorus and potassium. Agri. Res. J. Kerala. 24(2): 132-150.

Nybe, E.V. and Nair, P.C.S. 1987. Nutrient deficiency in black pepper (Piper nigrum L.). 2. Calcium, magnesium and sulfur. Agri. Res. J. Kerala. 25(1): 52-65.

O’Sullivan, J.N. ;Asher, C. J. ; Blamey, F.P.C. and Edwards, D.G. 1993. Mineral nutrient disorders of root crops of the Pacific: Preliminary observations on sweet potato (Ipomoea batatas). Plant and Soil. 155/156: 263-267.

Otani, T; Ae, N. and Tanaka, H. 1996. Phosphorus uptake mechanism of crops grown in soils with low P status II. Significance of organic acids in root exudates of pigeon pea. Soil Sci. Plant Nutr. 42: 553-560.

Owuoche, J.O. ; Briggs, K.G. ; Taylor, G.J and Penney, D.C. 1995. Response of eight Canadian spring wheat ( Triticum aestivum L. ) cultivars to copper: copper content in leaves and grain. Canadian J. Plant Sci. 75(2): 405-411.

Podlask, W.; Werner, T.; Grum, M.; Schlegel, R. and Hulgenhof, E. 1990. Genetic differences in the copper efficiency of cereals. M. L. Van Beusichem (Ed.), Plant Nutrition- Physiology and Application, Kluwer Academic Publishers. pp. 297-301.

Preeti, J. ; Mehrotra, S.C. and Jain, P. 1994. A critical evaluation of some nutrient ratios as indicators of iron chlorosis in plants. New Botanist. 21(1-4): 167-168.

Rengel, Z. 1997. Root exudation and microflora populations in rhizosphere of crop genotypes differing in tolerance to micronutrient deficiency. In: Plant Nutrition- for sustainable food production and environment, T. Ando et. al. (Eds), Kluwer Academic Publishers, Tokyo. 243-248.

Randall, P. J. 1995. Genotypic differences in phosphate uptake. In: Genetic manipulation of crop plants to enhance integrated nutrient management in cropping systems. I. Phosphorus: Proceedings of an FAO/ICRISAT Expert Consultancy Workshop. Johnson et al. (Eds.). pp 31-47 International Crop Research Institute for the Semi-Arid and Tropics, Patancheru, Andhra Pradesh, India

Razmjoo, K. ; Imada, T. ; Sugiura, J. and Kanek, S. 1997. Seasonal variations in nutrient and carbohydrate levels of tall fescue cvs. in Japan. J. Plant Nut. 20(12): 1667-1679.

Reddy, K.B. ; Ashalatha, M. and Venkaiah, K. 1993. Differential response of groundnut genotypes to iron stress. J. Plant Nut. 16(3): 523-531

Reddy, K. B.; Bhaskar, P. V. and Venkaiah, K. 1997. Iron stress response in iron-efficient and iron-inefficient groundnut cultivars. In: Plant Nutrition- for sustainable food production and environment, T. Ando et. al. (Eds), Kluwer Academic Publishers, Tokyo. 255-256.

Reddy, T.Y. and Reddi, G.H.S. 1997. Mineral nutrition, manures and fertilizers. In Principles of Agronomy. pp. 204-256.  Kalyani Publishers, Ludhiana, India.

Rengel, Z. 1995. Carbonic anhydrase activity in leaves of wheat genotypes differing in zinc efficiency. J. Plant Physiol. 147: 251-256.

Rengel, Z. and Graham, R. D. 1995. Wheat genotypes differ in Zn efficiency when grown in chelate-buffered nutrient solution. I. Growth. Plant and Soil. 176: 307-316.

Rengel, Z. and Graham, R. D. 1996. Uptake of zinc from chelate-buffered nutrient solutions by wheat genotypes differing in zinc efficiency. J Expt. Bot. 47: 217-226.

Roberts, S. and Rhee, J.K. 1990. Boron utilization by potato in nutrient cultures and in field plantings. Commun. Soil Sci. Plant Analysis. 21(11-12): 921-932.

Romheld, V. 1998. The soil-root interface (rhizosphere): Its relationship to nutrient availability and plant nutrition. In: International workshop on role of environmental and biological factors in acquisition of toxic and essential elements by plants. Research Institute of Pomology and Floriculture, Skierniewice. pp. 41-58.

Russelle, M.P. and McGraw, R.L. 1986. Nutrient stress in birdsfoot trefoil. Can. J. Pl. Sci. 66: 933-944.

Sabbe, W. E. and Batchelor, J. T. 1990. Yield and nitrogen concentrations in wheat (Triticum aestivum) as affected by split nitrogen application and growth stage. ). In: M. L. van Beusichem (Ed.), Plant nutrition- physiology and applications, Kluwer Academic Publishers, Dordrecht. 741-746.

Sahi, H.P.S.; Sharma, P.K. and Sachan, P.L. 1992. Check khaira disease of rice with zinc sulfate spray. Indian Farming. 41(11): 26.

Saric, M. R. 1987. Progress since the first international symposium : ‘Genetic aspects of plant mineral nutrition’. Beogard, 1982, and perspectives of future research. Plant and Soil. 99: 197-209.

Saxena, M.C. ; Mehrotra, R.S. and Singh, K.B. 1990. Iron deficiency in chickpea in the Mediterranean region and its control through resistant genotypes and nutrient application. Plant and Soil. 123(2): 251-254.

Scaife, M.A. and Clarkson, D.J. 1979. Calcium related disorders in plants – a possible explanation for the effect of weather. Plant and Soil. 50(3): 723-725.

Schenk, M. K. and Barber, S. A. 1979. Root characteristics of corn genotypes as related to phosphorus uptake. Agron. J. 71: 921-924.

Sekhon, G.S.1999. Potassium in Indian soils and crops. Procc. of the Indian National Sci. Academy. Part B, Reviews & Tracts Biological Sci. 65(3-4): 83-108.

Sharma, A.K. Singh, R.; Singh, U.S. and Singh, R. 1988. Effect of vescicular arbuscular mycorrhiza on uptake of phosphorus and zinc in rice (Oryza sativa L.). Current Sci. 57(16): 901-902.

Shelp, B.J.; Shattuck, V.I. and Proctor, J.T.A. 1987. Boron nutrition and mobility and its relation to the elemental composition of greenhouse grown root crops.2.Radish. Commun. in Soil Sci. and Plant Analysis. 18(2): 203-219.

Shimada, N. and Ando, T. 1980. Role of nickel in plant nutrition (2). Effect of nickel on the assimilation of urea by plants. Jpn. J. Soil Sci. Plant Nutr. 51: 493-496.

Silva, H. and Rodrigue, J. 1996. Physiological disorders of Pomaceae fruit induced by calcium deficiency. An integrated focus on the problem. Revista Fruticola.17(1): 5-17

Simon, J.E. ; Wilcox, G. E. ; Simini, M. ; Elamin, O.M. and Decoteau, R.D. 1986. Identification of manganese toxicity and magnesium deficiency on melons grown in low-pH soils. HortScience. 21(6): 1383-1386.

Singh, A. L. and Joshi, Y.C.1997. Prevention and correction of iron-deficiency chlorosis of groundnut in India. In: Plant Nutrition- for sustainable food production and environment, T. Ando et. al. (Eds), Kluwer Academic Publishers, Tokyo. 271-272.

Smith, G.S. ; Clark, C.J. and Holland, P.T. 1987. Chlorine requirement of kiwifruit (Actinidia deliciosa). New Phytologist. 106(1): 71-80.

Sonneveld, C. and Voogt, W. 1991. Effects of Ca-stress on blossom-end rot and Mg-deficiency in rockwool grown tomato. Acta Hort. 294: 81-88.

Spehar, C.R. and Galwey, N.W. 1997. Screning soybean (Glycine max L. Merrill) for calcium efficiency by root growth in low Ca nutrient solution. Euphytica. 94(1): 113-117.

Stuiver, C.E.E. ; Kok, L.J. ; Westerman, S. and Dekok, L.J. 1997. Sulfur deficiency in Brassica oleracea L : Development, biochemical characterisation and sulfur/nitrogen interactions. Russian J. Plant Physiol. 44(4): 505-513.

Swietlik, D. 1995. Interactions between zinc deficiency and boron toxicity on growth and mineral nutrition of sour orange seedlings. J. Plant Nut. 18(6): 1191-1207.

Tamada, T. 1989. Nutrient deficiency of rabbiteye and highbush blue barries. Acta Hort. 241: 132-138.

Trull, M.C.; Guitinan, M.J.; Lynch, J.P. and Deikman, J. 1997. The response of wild type and ABA mutant Arabidiopsis thaliana plants to phosphorus starvation. Plant cell and environment. 20(1): 85-92.

Whitehead, D.C. 1985. Chlorine deficiency in red clover grown in solution culture. J. Plant Nutr. 8(2): 193-198.

Xu, G.; Magen, H.; Tarchitzky, J. and Kafkafi, U. 2000. Advances in chloride nutrition of plants. Adv. Agron. 68: 97-150. 

Yu, Q. and Rengel, Z. 1999. Micronutrient deficiency influences plant growth and activities of superoxide dismustases in narrow-leafed lupines. Ann. Bot. 83(2): 175-182.

Yu, X. ; Bell, P.F. and Yu, X.O. 1998. Nutrient deficiency symptoms and boron uptake mechanism of rice. J. Plant Nut. 21(10): 2077-2088.

Zaiter, H.Z. and Ghalayini, A. 1994. Iron deficiency in lentils in the Mediterranean regions and its control through resistant genotypes and nutrient application. J. Plant Nut. 17(6): 945-952.